Problem 1 - Word Search

Question

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

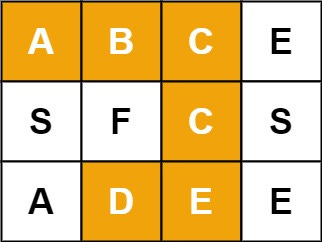
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

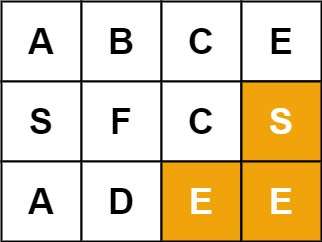
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

Constraints:

• m = board.length

• n = board[i].length

• 1 <= m, n <= 6

• 1 <= word.length <= 15

• board and word consists of only lowercase and uppercase English letters.

Approach

This solution utilizes a depth-first search (DFS) approach to search for the given word on the board. It checks each cell in the board and recursively explores its neighboring cells to find a valid path that matches the characters of the word. If a valid path is found, it returns true; otherwise, it returns false.

Here's a summary of the DFS algorithm for this solution:

1. Start iterating over each cell in the board.

2. For each cell, perform a DFS search to check if it forms a valid path for the word.

3. During the DFS search, check if the current cell matches the character of the word at the corresponding index. If not, return false.

4. Mark the current cell as visited (or replace its value temporarily) to avoid revisiting it.

5. Recursively perform DFS searches on the neighboring cells (up, down, left, and right) to find the next character of the word.

6. If a valid path is found (all characters of the word are matched), return true.

7. If no valid path is found from the current cell, backtrack by unmarking the current cell and continue the search from the previous cell.

8. Repeat steps 2-7 for all cells in the board.

9. If no valid path is found from any cell, return false.

By applying this DFS approach, the program checks if the given word can be formed by moving through adjacent cells in the board.

Solution

Solve it here

class Solution {
    public boolean exist(char[][] board, String word) {
        if (board == null || board.length == 0 || board[0].length == 0 || word == null || word.length() == 0) {
            return false;
        }

        int rows = board.length;
        int cols = board[0].length;

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (dfs(board, i, j, word, 0)) {
                    return true;
                }
            }
        }

        return false;
    }

    private boolean dfs(char[][] board, int row, int col, String word, int index) {
        if (index >= word.length()) {
            return true;
        }

        int rows = board.length;
        int cols = board[0].length;

        if (row < 0 || col < 0 || row >= rows || col >= cols || board[row][col] != word.charAt(index)) {
            return false;
        }

        char temp = board[row][col];
        board[row][col] = '#';

        boolean found = dfs(board, row + 1, col, word, index + 1) ||
                        dfs(board, row - 1, col, word, index + 1) ||
                        dfs(board, row, col + 1, word, index + 1) ||
                        dfs(board, row, col - 1, word, index + 1);

        board[row][col] = temp;
        return found;
    }
}

Time and space complexity

Time Complexity: The time complexity of this solution is O(N * 3^L), where N is the total number of cells in the board and L is the length of the word. The algorithm iterates through each cell in the board (N iterations), and during the DFS search, it explores up to three neighboring cells (3^L). As the word length increases, the number of recursive calls and explorations increases exponentially.

Space Complexity: The space complexity of this solution is O(L), where L is the length of the word. The space is used for the recursive stack to track the depth of the DFS search. In the worst case, when the length of the word is the same as the number of cells visited during the search, the space complexity is O(L). Additionally, a constant amount of extra space is used for temporary variables.

It's worth noting that the space complexity can be further optimized by using an in-place marking approach instead of using a separate visited array, which would reduce the space requirement to O(1). However, the time complexity would remain the same.

---