Problem 12 - Sum of Left Leaves

Explore our archive for previous posts.

Question

Given the root of a binary tree, return the sum of all left leaves.

A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.

Example 1:

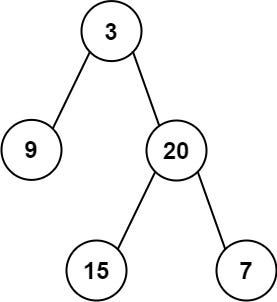
Input: root = [3,9,20,null,null,15,7]
Output: 24
Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Example 2:

Input: root = [1]
Output: 0

Constraints:

• The number of nodes in the tree is in the range [1, 1000].

• -1000 <= Node.val <= 1000

Approach

This solution uses a recursive approach to calculate the sum of left leaves in a binary tree. Here's a breakdown of the steps:

1. If the current node is null, return 0. This serves as the base case for the recursive calls.

2. If the left child of the current node exists and is a leaf node (i.e., its left and right children are null), return its value plus the sum of left leaves in the right subtree. This accounts for the case where the left child is a valid left leaf.

3. If the left child is not a leaf node, recursively calculate the sum of left leaves in the left and right subtrees by making recursive calls to sumOfLeftLeaves().

4. Return the sum of left leaves in the left and right subtrees.

Solution

Solve it here

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        // Base case: if the current node is null, return 0
        if (root == null) {
            return 0;
        } else if (root.left != null && root.left.left == null && root.left.right == null) {
            // If the left child of the current node exists and is a leaf node,
            // return its value plus the sum of left leaves in the right subtree
            return root.left.val + sumOfLeftLeaves(root.right);
        } else {
            // Recursively calculate the sum of left leaves in the left and right subtrees
            return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
        }
    }
}

Time and space complexity

Time Complexity: The time complexity of the solution can be expressed as O(n), where n is the number of nodes in the binary tree. This is because in the worst case, we need to visit every node in the tree once to calculate the sum of left leaves.

Space Complexity: The space complexity of the solution can be expressed as O(h), where h is the height of the binary tree. In the worst case, if the binary tree is skewed and resembles a linked list, the height of the tree can be n, where n is the number of nodes. The space occupied by the recursive calls on the stack is proportional to the height of the tree. It's important to note that the space complexity for the recursive solution is determined by the height of the tree rather than the number of nodes. If the binary tree is balanced or has a small height, the space complexity will be relatively small. However, if the tree is highly unbalanced, with a height close to the number of nodes, the space complexity will be closer to O(n), where n is the number of nodes.