Problem 20 - Symmetric Tree

Explore our archive for previous posts.

Question

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Example 1:

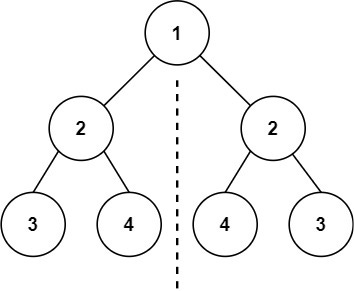
Input: root = [1,2,2,3,4,4,3]
Output: true

Example 2:

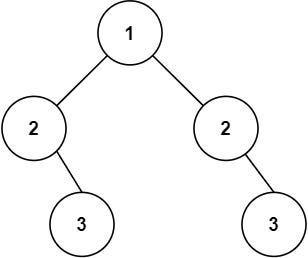
Input: root = [1,2,2,null,3,null,3]
Output: false

Constraints:

• The number of nodes in the tree is in the range [1, 1000].

• -100 <= Node.val <= 100

Approach

This problem is similar to another problem discussed in a previous edition. Please check that out to get a better understanding of this problem.

The given solution checks if a binary tree is symmetric by recursively comparing its left and right subtrees. The isSymmetric method handles the base case of a null root and calls the isMirror method to check for mirror symmetry between the left and right subtrees. The isMirror method checks if both nodes are null or have different values and recursively compares the left subtree of the first node with the right subtree of the second node, and vice versa.

In the isMirror method, we follow similar logic as in the "Same Tree" problem. We check if both nodes are null, or if their values are different. If any of these conditions are true, it means the subtrees are not mirrors of each other, so we return false. The difference between this solution and the “Same tree” solution is that here, we recursively call the isMirror method for the left subtrees (node1.left and node2.right) and the right subtrees (node1.right and node2.left). If both recursive calls return true, it means the subtrees are symmetric. In that case, we can conclude that the overall tree is symmetric, and we return true.

Solution

Solve it here

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        
        return isMirror(root.left, root.right);
    }
    
    private boolean isMirror(TreeNode node1, TreeNode node2) {
        // Base case: Both nodes are null, so they are considered symmetric
        if (node1 == null && node2 == null) {
            return true;
        }
        
        // Check if either node is null or their values are different
        if (node1 == null || node2 == null || node1.val != node2.val) {
            return false;
        }
        
        // Recursively check the left and right subtrees
        return isMirror(node1.left, node2.right) && isMirror(node1.right, node2.left);
    }
}

Time and space complexity

Time Complexity: The time complexity of this solution is O(n), where n is the total number of nodes in the binary tree. This ie because we need to visit each node once to compare their values.

Space Complexity: The space complexity is O(h), where h is the height of the tree. In the recursive calls, the space required for the call stack is proportional to the height of the tree. In the worst case, if the tree is skewed and has a height of n, the space complexity becomes O(n). However, in the average case, the space complexity is O(log n) for balanced trees.