Problem 34 - Interleaving String

Explore our archive for previous posts.

Problem 33 - Edit Distance

Problem 32 - Remove Duplicates from Sorted Array

Question

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2. An interleaving of two strings s and t is a configuration where s and t are divided into n and m substrings respectively, such that:

• s = s1 + s2 + ... + sn

• t = t1 + t2 + ... + tm

• |n - m| <= 1

• The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...

Note: a + b is the concatenation of strings a and b.

Example 1:

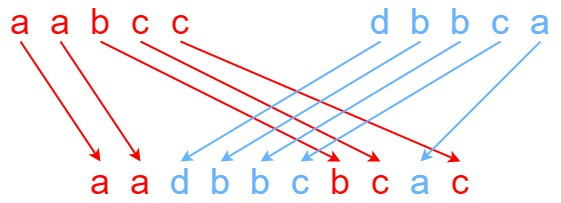
Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true
Explanation: One way to obtain s3 is:
Split s1 into s1 = "aa" + "bc" + "c", and s2 into s2 = "dbbc" + "a".
Interleaving the two splits, we get "aa" + "dbbc" + "bc" + "a" + "c" = "aadbbcbcac".
Since s3 can be obtained by interleaving s1 and s2, we return true.

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false
Explanation: Notice how it is impossible to interleave s2 with any other string to obtain s3.

Example 3:

Input: s1 = "", s2 = "", s3 = ""
Output: true

Constraints:

• 0 <= s1.length, s2.length <= 100

• 0 <= s3.length <= 200

• s1, s2, and s3 consist of lowercase English letters.

Approach

We’ll use dynamic programming to solve this problem. The approach involves constructing a 2-D DP array where dp[i][j] indicates whether the first i characters of s1 and the first j characters of s2 can interleave to form the first i + j characters of s3. The DP array is filled iteratively, considering three possibilities:

1. If the i-th character of s1 matches the i + j-th character of s3.

2. If the j-th character of s2 matches the i + j-th character of s3.

3. A combination of both matches.

The DP array helps determine whether it's possible to create s3 by interleaving s1 and s2. The solution returns true if such interleaving is possible; otherwise, it returns false.

Solution

Solve it here

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        // Return false if lengths of s1 and s2 don't add up to s3
        if (s1.length() + s2.length() != s3.length()) return false;
        
        int m = s1.length(); // Length of s1
        int n = s2.length(); // Length of s2

        boolean[][] dp = new boolean[m + 1][n + 1]; // dp[i][j] represents if the first i characters of s1 and the first j characters of s2 can interleave to form the first (i + j) characters of s3

        dp[0][0] = true; // An empty s1 and s2 can interleave to form an empty s3
        
        // Fill in the first row of the matrix
        for (int i = 1; i <= m; i++) {
            dp[i][0] = dp[i - 1][0] && (s1.charAt(i - 1) == s3.charAt(i - 1));
        }
        
        // Fill in the first column of the matrix
        for (int i = 1; i <= n; i++) {
            dp[0][i] = dp[0][i - 1] && (s2.charAt(i - 1) == s3.charAt(i - 1));
        }
        
        // Fill in the rest of the matrix
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = (dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)) || (dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));
            }
        }
        
        return dp[m][n]; // The result is stored in dp[m][n]
    }
}

Time and space complexity

Time Complexity: The time complexity is O(m * n), where m and n are the lengths of strings s1 and s2. This is because we use a 2D matrix to compare characters in both strings with string s3.

Space Complexity: The space complexity is O(m * n) as well, as we use a 2D array of this size to store intermediate results.

Explore more?

Missed a previous edition? Catch up on the insightful content you might have missed by visiting our archive here. Thank you for being a valued reader of our newsletter. We appreciate your continued support!

Want free mock interviews?

Simply share our newsletter with your friends, colleagues, or anyone you think would love our coding insights.

When your friends use your referral link to subscribe, you’ll receive special benefits.

• Get a free mock coding interview for 10 referrals

• Get a 1:1 coding Q&A session for 15 referrals

• Get a guest post opportunity for 25 referrals