Problem 4 - Container with most water

Question

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1:

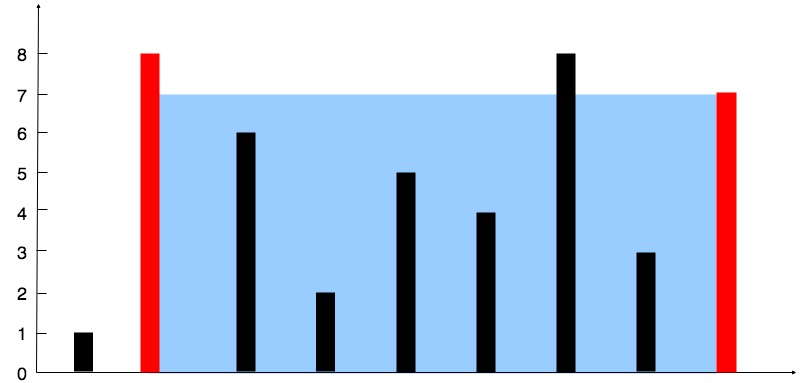
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

Input: height = [1,1]
Output: 1

Constraints:

• n == height.length

• 2 <= n <= 105

• 0 <= height[i] <= 104

Approach

This solution utilizes the two-pointer approach to find the maximum area between two vertical lines. It starts with two pointers, left and right, pointing to the first and last elements of the array, respectively. The maximum area is initially set to 0.

The algorithm then iterates while the left pointer is less than the right pointer. It calculates the current area by taking the minimum height between the two pointers and multiplying it by the distance between them. If the current area is greater than the maximum area found so far, it updates the maximum area.

To maximize the area, the algorithm moves the pointer that corresponds to the shorter height. This is because the area is limited by the shorter height, and moving the pointer with the taller height would only decrease the area further. The algorithm continues this process until the left and right pointers meet.

Finally, it returns the maximum area obtained.

Solution

Solve it here

class Solution {
    public int maxArea(int[] height) {
        int maxArea = 0;
        int left = 0;
        int right = height.length - 1;

        while (left < right) {
            int currentArea = Math.min(height[left], height[right]) * (right - left);
            maxArea = Math.max(maxArea, currentArea);

            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }

        return maxArea;
    }
}

Time and space complexity

Time Complexity: The time complexity of this solution is O(N), where N is the number of elements in the input array. This is because the solution performs a single pass through the array, comparing the areas and moving the pointers until they meet.

Space Complexity: The space complexity of the solution is O(1), meaning it uses a constant amount of extra space. This is because the solution only utilizes a few variables to track the pointers and the maximum area, and does not require any additional data structures that grow with the input size.