Explore our archive for previous posts.
Question
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
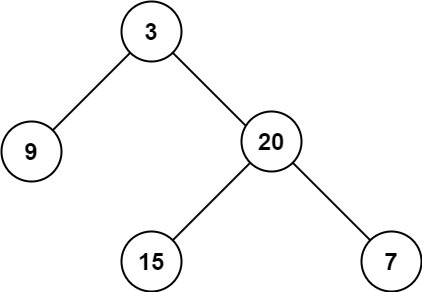
Example 1:
Input: root = [3,9,20,null,null,15,7]
Output: 3Example 2:
Input: root = [1,null,2]
Output: 2Constraints:
The number of nodes in the tree is in the range
[0, 10^4].-100 <= Node.val <= 100
Approach
This problem involves finding the maximum depth or height of a binary tree. Here's a high-level approach:
Base Case: If the root is null, the depth is 0.
Recursive Case: Calculate the depth of the left and right subtrees recursively.
Return Maximum: Return the maximum depth of the left and right subtrees plus 1 (for the current level).
Solution
Solve it here
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
public class Solution {
public int maxDepth(TreeNode root) {
// Base case: if the root is null, the depth is 0
if (root == null) {
return 0;
}
// Recursive case: calculate the depth of left and right subtrees
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
// Return the maximum depth of left and right subtrees plus 1 for the current level
return Math.max(leftDepth, rightDepth) + 1;
}
}Time and space complexity
Time Complexity: The time complexity of this algorithm is O(n), where n is the number of nodes in the binary tree. Each node is visited exactly once.
Space Complexity: The space complexity is O(h), where h is the height of the binary tree. In the worst case, the space required is the height of the tree, which is equivalent to the maximum depth of the recursion stack.
Explore more?
Missed a previous edition? Catch up on the insightful content you might have missed by visiting our archive here. Thank you for being a valued reader of our newsletter. We appreciate your continued support!
Great walkthrough! How often do you think this type of recursion trips up even strong candidates?